
In October 1884, at the invitation of the President of the United States, 41 delegates from 25 nations met in Washington, DC, for the International Meridian Conference. Conference resolutions 1 to 3 dealt with standardizing geographic coordinates. It was resolved that "It was desirable to adopt a single world meridian to replace the numerous one's already in existence. 2.The Meridian passing through the principal Transit Instrument at the Observatory at Greenwich was to be the 'initial meridian' and 3.That all longitude would be calculated both east and west from this meridian up to 180°." Resolution 2, fixing the Meridian at Greenwich was passed 22-1 (San Domingo voted against), France & Brazil abstained (Howse, 1997, p. 141). Thus the Meridian conference established two criteria for acceptance of geographic coordinates as a global geocoding system. These were its universality (by determining its scope of application and origin) and authority (by the acts of resolving and voting at an international conference).
This paper examines briefly the criteria that a global geocoding system or geographical reference frame strives for. These criteria are recounted here not out of originality, but with the intent of providing a framework against which individual geocoding systems can be compared. Furthermore, since qualitative comparisons serve primarily to stimulate debate rather than good science, a set of metrics is proposed so that each existing and new system alike can be measured against the remainder and against definitive absolute metrics. To illustrate the approach, these metrics are computed for a selected small set of existing global grid systems and the results presented for discussion. It is hoped that presenting the metrics and their means of computation will stimulate analytical studies of global grid systems, to refine their applicability and characteristics, and to aid the map user in their selection for a particular purpose.
Table 1: Comparison of Criteria for the Assessment of Global Grids
| Criteria in Goodchild (1994) | Criteria in Kimerling et al. (1999) (Goodchild's Numbers given in parentheses) |
| 1. Each area contains one point | Areal cells constitute a complete tiling of the globe, exhaustively covering the globe without overlapping. (3,7) |
| 2. Areas are equal in size | Areal cells have equal areas. This minimizes the confounding effects of area variation in analysis, and provides equal probabilities for sampling designs. (2) |
| 3. Areas exhaustively cover the domain | Areal cells have the same topology (same number of edges and vertices). (9, 14) |
| 4. Areas are equal in shape | Areal cells have the same shape. ideally a regular spherical polygon with edges that are great circles. (4) |
| 5. Points form a hierarchy preserving some (undefined) property for m < n points | Areal cells are compact. (10) |
| 6. Areas form a hierarchy preserving some (undefined) property for m < n areas | Edges of cells are straight in a projection. (8) |
| 7. The domain is the globe (sphere, spheroid) | The midpoint of an arc connecting two adjacent cells coincides with the midpoint of the edge between the two cells. |
| 8. Edges of areas are straight on some projection | The points and areal cells of the various resolution grids which constitute the grid system form a hierarchy which displays a high degree of regularity. (5,6) |
| 9. Areas have the same number of edges | A single areal cell contains only one grid reference point.(1) |
| 10. Areas are compact | Grid reference points are maximally central within areal cells. (11) |
| 11. Points are maximally central within areas | Grid reference points are equidistant from their neighbors. (12) |
| 12. Points are equidistant | Grid reference points and areal cells display regularities and other properties which allow them to be addressed in an efficient manner. |
| 13. Edges are areas of equal length | The grid system has a simple relationship to latitude and longitude. |
| 14. Addresses of points and areas are regular and reflect other properties | The grid system contains grids of any arbitrary defined spatial resolution. (5,6) |
This study hopes to build upon this pioneering research. In Kimerling et al.'s rebuilding of the criteria, two factors emerged. First, that metrics are critical to implementing and using the criteria effectively. Second, that while commonalties have emerged between the two versions of the Goodchild criteria, nevertheless the Kimerling et al.'s work was oriented primarily toward hierarchical recursive global grids. An attempt is made here, therefore, to be both more specific in terms of metrics, and more general in terms of criteria. Furthermore, criteria that relate to geometry rather than topology (such as Kimerling's seventh and Goodchild's eighth) are specific to projection properties rather than grid characteristics. In many grids, a projection is assumed, and recursion takes place on the plane. The grid's relation to projection distortion is then a given. This is because Goodchild's properties 2, 4, 8, 9, 10, 12, and 13 are consequences of the projection decision and the assumption of the earth model, not necessarily the grid systematics. This is the case even with geographic coordinates.
The approach taken here is more generic, and includes more of a grid system user orientation than an algorithmic, topological, or computational geometric perspective. It is hoped that a user based grid comparison will be of use in the grid selection process, and assist users in learning grid systems. First, the dimensions of the criteria are considered, and some metrics identified. These are collected into a single framework, and some examples given for specific grids.
Related to the universality dimension is the ability to recover the system from empirically derivable features. Examples are the poles, the equator and universal time, all of which are absolute and measurable given the right algorithm. Actual origins, however, may or may not be tied to tangible features. Perhaps the most universal of systems is geographic coordinates, which applies to all three earth models and to the whole planet. Nevertheless, its origin point (Figure 1) is recoverable only with extensive use of sophisticated navigation equipment and/or astronomical observation. A first metric of universality, therefore, might be the degree or ease of recoverability of the primary reference monuments and the linear dimensions for the system.

Figure 1. Origin Point of the Geographic Coordinate System (0 degrees North, 0 degrees East)
On the purely practical level, universality also relates to the adoption of standards. International Standards Organization (ISO) standards represent the peak of a hierarchy that moves through national standards such as ANSI, all the way to "industry" standards and de facto standards such as PostScript. Some measure of universality, therefore, should reflect the incorporation of broadly acceptable standards. This may include the use of the decimal system, use of metric units, use of Arabic numbers (0,1,2,3... etc.), and the specification of a reference ellipsoid by an international body. For example, WGS84 is broadly accepted and used as a reference ellipsoid, though its exact specification remains classified. A higher standard is the International Earth Rotation Service's International Terrestrial Reference System (ITRS). A second measure of universality therefore, might be the number of geocoding system parameters that are tied to standards, weighted for the level of the standard.
In addition, universality applies to the extent of the system's actual coverage. In UTM, for example, coverage extends from 84 degrees North to 80 degrees South, leaving the UPS for polar coverage. While UTM covers just about all of the earth's inhabited area, nevertheless the real extent is incomplete, depending on the UPS to fill the gaps. A metric corresponding to the extent of coverage might be the actual land area of the terrain "covered" by the grid, as a ratio to the total surface area of the earth model or ellipsoid. This metric is reconsidered under the dimension of exhaustiveness.
Formalization into standards, such as FIPS 173, at the national level moves the system to the next level of credibility. Beyond national standards lie those of international collaboratives (e.g. scientific or professional societies, NATO), then the official recognition of International Standards bodies and the United Nations. The so-called Peters projection, for example, was less than a historical footnote until Peters convinced the World Council of Churches and the United Nations to endorse the map (Monmonier, 1995).
At the highest level of recognition lies acceptance by the International Standards Organization (ISO), and by consortia of professional societies at the international level and acceptance for extended periods of time. For example, the International Earth Rotation Service (IERS) was created in 1988 by the International Union of Geodesy and Geophysics (IUGG) and the International Astronomical Union. It replaced the Earth rotation section of the Bureau International de l'Heure, and the International Polar Motion Service. IERS is a member of the Federation of Astronomical and Geophysical Data Analysis Services and has been established since 1988 to provide to the worldwide scientific and technical community reference values for Earth orientation parameters and reference realizations of internationally accepted celestial and terrestrial reference systems. The IERS is charged to define, use and promote the International Terrestrial Reference System (ITRS) as defined by the IUGG resolution No 2 adopted in Vienna in 1991.
Another type of authority is that of broad popular acceptance and use. Map users are highly influenced by choices make by the map production agencies. The United States Geological Survey, for example, normally marks geographic coordinates, UTM, and State Plane coordinates on the collars of its topographic quadrangle maps at 1:24,000. City Street Guides commonly use one-off Alphabet-Number referencing. Neither group based the choice of systems that the map consumer must use by practical necessity on user demand assessment, although the USGS has occasionally changed grids and their depiction at the request of its fellow federal agencies such as the US Forest Service. Acceptance of systems is probably highest with street referencing, involving common use and standardization by the US Post Office, and including extensive international cooperation.
Measures of authority are necessarily subjective, since they are based primarily on trust. A simple measure would be the hierarchical level in the schema from individual to global organization. Another would be the customer acceptance, in terms of market share. A simple alternative metric would be the number of standards that form the definition of a particular grid system, or conversely, the number of standards that use a system for defining geographical referencing.
Communication theory provides a measure of the quantity of information that flows during a transmission from sender to receiver (Shannon, 1948). Transmission flows involving coordinates are common, for example when GPS data are collected, when search and rescue operations are conducted, or when GIS coordinate based data are moved between systems or used over a network. The general formula for reducing the uncertainty of communication to zero ("computing the amount of information generated by the reduction of n possibilities (all equally likely) to 1." Dreske, 1999) or the entropy, is given by the base 2 log of n. This value, in bits, is the necessary length of a binary number that fully defines an atomic unit in the system undergoing transmission. In the case of coordinates, this is a point. We will consider only the case of two coordinates, in spite of the fact that three coordinates strictly are necessary to define location (the reference ellipsoid is assumed instead of the geoid).
A paradox of grid coordinate systems is that points located close to each other in geographic space have similar coordinates. This is a corollary of Tobler's famed "first law of geography," that everything is related to everything else, but near things are more related than distant things (Tobler, 1970). If indeed the importance of discrimination of locations is equally important as points become closer together, say for local navigation, then the redundancy within the coordinates becomes a maximum, when it would be best be minimum.
Tukey (1977) advanced the stem-and-leaf plot as a simple tool for finding the level of redundancy in transmissions. Shannon (1948) had previously devised a mathematical theory of information in communication that related the amount of information transferred to the reduction of the uncertainty at the receiver end of the transmission. Such an approach can be used with coordinates in a global grid system. For example, as a map user parses along a vector, information is sequentially extracted from strings of coordinate pairs that carry geographic information content, usually coded from left to right, but sometimes interwoven and alternating digits. As each successive digit (or bit) is traversed, more spatial information flows, and serves the function of distinguishing the current point from the previous point. Similarly, we can talk about the set of points constituting a geographic feature, whether it be a point, line, area or compound feature.
For a set of geographic coordinates, a ratio can be defined that is the measured range, standard deviation, and maximum possible range of each coordinate. For example, for the set of coordinates {632794.69 4538257.50 632948.69 4538520.00 632554.25 4538098.50 632794.69 4538257.50 632231.31 4537331.00 632554.25 4538098.50} which constitute UTM coordinates in Zone 18, Northern hemisphere, forming a small part of the outline of Long Island, we can compute the following values:
Table 2. Statistical Description of Six Coordinate pairs in UTM
| Minimum (x, y) | Maximum | Range (m) | Standard Deviation (m) | Std. Dev as Proportion of Range | Zone 18, N |
| 632231.31 | 632948.69 | 717.38 | 232.609114 | 0.32425 | UTM Easting |
| 4537331.00 | 4538520.00 | 1189.00 | 369.041521 | 0.31038 | UTM Northing |
These estimates of total range and variance, however, mask the variance structure as it relates to the coordinates digits themselves. Accordingly, consider that for every significant digit of the coordinate there is both an actual and an expected proportion of the coordinate count within the set. For the ten digits of decimal numbers, if over the set the actual proportional occurrence of each digit, "0", "1", "2" and so forth was the same as the expected (0.1) then the sum of the deviations would be zero. If all coordinate digits were identical in occurrence across points, then nine digits would have no occurrence (0.0 - 0.1 x 9 = -0.9) and one digit would have the whole point set (1.0 - 0.1 = 0.9), whose magnitudes sum to 1.8. This is the case for the first three digits of both the easting and the northing in the set. Thus digit variances would vary from zero (for no difference between expected and actual digit occurrence) and 1.8, when all digits are identical. The equivalent values are 1.875 for hexadecimal, 1.75 for octal and 1 for binary, given by 2 (B-1)/B where B is the number base. For any digit n at any one significant digit location out of N possible digit values or states (10 for decimal), I is defined, where:
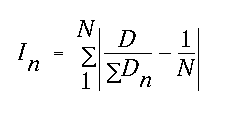
Similarly, the set of these values across all significant digits defines a function that starts at complete redundancy, drops as the information content increases, then returns to near redundancy in this case beyond the decimal point. This might be termed the Coordinate Digit Density function. The "area" or total divergence of this function from complete redundancy defines a value which is an entropy or information quantity value for the coordinate set which may be independent of the coordinate system and therefore of value in comparison. This value, termed S, for N significant digits and assuming number base B is given by:
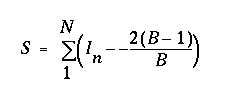
Computing S for the six point set above yields 2.167 for the northings and 2.407 for the eastings. Both eastings and northings have their highest maximum entropy at the third decimal place, and have five redundant digits. The Coordinate Digit Density functions are shown in figure 2.
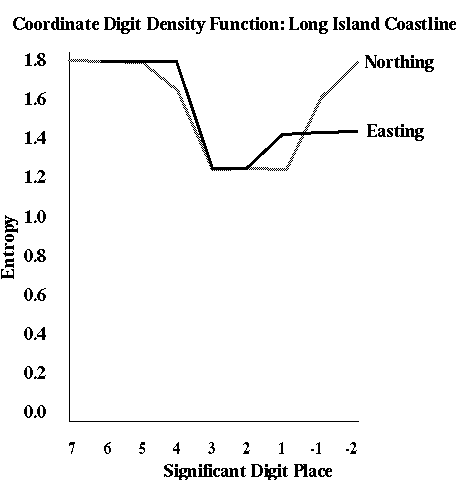
Figure 2. Coordinate Digit Density Function
The easting and northings show some differences, which for a larger point sample may be worth investigating. For example, neither reaches a value below 1.0, which might be expected at the peak information content digit near the decimal place. The first three and last digits of the northing and the first three digits of the easting are redundant. Any compression system, such as leaving off the zone number and a 100 km intersection reference and truncation of redundant decimal places would compress the data to those digits below the 1.8 line. Significantly, the abbreviation of the northing to the nearest 0.5 meter and the repetitive rounding of the northing imply that the data have been converted from other units or degrees (they were).
The measure S, and the Coordinate Digit Density function are proposed as useful means for the comparison of global grid systems. Since the density function depends only on frequencies, letters and other systems, such as octal, binary and hexadecimal are equally suited to the metric. Comparison is possible between and among the same exact position in different systems, set of positions in different systems, or coordinate extremes. Simple statistical description implied that the northing had a much higher variation in range and standard deviation, but a lower deviation as a proportion of the range. The digit analysis shows that the eastings have a higher information content, and that it is concentrated between the fourth digit and second decimal place, i.e. in the 1km to 1cm range.
A succinct coordinate system, therefore, is one with the most spiked coordinate digit density function, the lowest entropy associated with a single coordinate digit, and the highest S. Nevertheless, this ignores the fact that many coordinate systems are hierarchical. While the measure applies equally well to almost all systems, it is possible to score the levels of the hierarchy independently, to measure the bits required per level (using Shannon's formulae), and to estimate the total information content of a set of coordinates in different systems.
While succinctness depends heavily on assessing the total amount of information in coordinates, there are at least two other measures that may be critical for comparing systems. The first of these is retrieval time, that is the amount of time it takes to move an encrypted coordinate into a system where it can be readily interpreted. This can be considered in several ways. At the simplest, it is a simple number of algorithm steps, computations or look-ups necessary to write a coordinate into ASCII digits. So, for example, a transformation of coordinates may involve a decompression, binary to decimal conversion, bounds checks and an affine transformation. This could be quantified as a number of steps or as real CPU seconds. Secondly, use time is the opposite transformation as applied to the user of the grid system. How long would it take a novice or skilled map user to place the point onto a map, or encode a given location? This could be assessed subjectively, or measured in real seconds by testing map users.
Lack of overlap reduces redundancy, but may be an integral part of the grid system. Equally as important to the amount of overlap is the lack of confusability between higher orders of coordinates. For example, within a UTM zone (and even between systems, such as USPLS in meters) there is little to distinguish between zones. The Military Grid system recognizes this by assigning letter references and redundant discriminators to the UTM zone number, which usually has only one digit offset. Thus an effective grid system never creates coordinates for nearby points that have lower order northing and easting coordinate specifications that are similar. This argues for integrated hierarchies in coordinates, so that the confusion is explicitly eliminated. It is also supportive of those georeference systems that interleave eastings and northings.
Similarly, a global grid system should be able to support objects of different dimensions. Here the largest difference is the treatment of the coordinates themselves. In the Military Grid and the British National Grid, the reference unit is of varying area depending on the interwoven number of digits employed. While this works well for many applications, it is usually not sufficient for mixed point, line and area objects.
Exhaustiveness may or may not scale. For example, UTM is not exhaustive on a global level, even within a zone, but has redundant coverage at the edges of zones. Thus exhaustiveness should be assessed both at the global level and the local level in a hierarchical system, perhaps at every level. Similarly, grid exhaustiveness may be a function of the resolution of the atomic grid unit. Obviously as resolution becomes coarser, assigning grids to features involves overlap, redundancy and drop out. Some measures of this exhaustiveness have been quantified by Mulcahy (1999).
Finally, a grid system should be able to store sufficient precision to ensure exhaustiveness. At least, this means that atomic features (for example, bench marks, survey points, pixels on high resolution images, utility features such as power poles and manholes) must have a unique location. A better condition might be that the precision associated with the atomic unit for the grid is close to the accuracy of the measurement instruments. The latter implies an "effective resolution" that might be concisely delimited using the sampling theorem (Tobler, 2000). As a rule of thumb, the grid "spacing" or level at which precision is capable of feature discrimination should be less than half the average size of the smallest feature that the system is designed to locate. There are standard measures of precision and accuracy (Goodchild and Gopal, 1989). Relating these to the grid's effective atomic unit via the sampling theorem might be best done with a simple ratio.
Joints are where tiles meet on the ground. If joints overlap, tiles or zones interleave to form zones of a lack of definitiveness and redundancy. The geometry of the overlap and joints is important for accuracy, scale, direction, area and shape on the grid. These properties have long been quantified and even cartographically symbolized on maps (Mulcahy and Clarke, 2001). A metric of jointing should simply reflect the amount and distribution of joins in the system. This is given by (1) the number of recursive tilings used to reference the atomic unit in the grid and (2) the total number and length of tile edges in the entire system. This refers to all appropriate unique hierarchical levels, and may be computed as a function of level. The Quaternary Triangular Mesh (Dutton, 1999) for example, does not vary with recursion beyond the level one partition into triangles from the globe, nor does the quad tree approach of Tobler and Chen (1986). UTM has only 60 interior and 120 exterior edges at the highest (zone) division. Thus UTM could be said to score 180 on the zone edge scale.
Measuring intuition is perhaps hardest of all of the measures proposed! One set of ways of quantifying intuition is to count the impediments to use of the system. Possible metrics are (1) the number of separate "facts" necessary to learn or explain the system; (2) The number of "magic numbers", i.e. constants, arbitrary origin points, earth radii etc. necessary to define the system or to locate a single point within it; (3) The average number of words or pages that a software manual, textbook, or help system must devote to explaining the system to a user.
Harder to quantify are metrics that define the time necessary for fluency in the system (say, to achieve making no errors per 1,000 point fixes) by book learning or experience. Among these are the level (elementary school, junior high, high school, college) at which education is possible, the reading grade level necessary to understand system documentation, the time required for explanation of the grid, and the amount of retraining required for maintenance of the knowledge.
Another important property of global grids is their memorability. This property is not the memorability of the systematics of the system, but the memorability of the georeferences themselves. For example, it is relatively easy to remember that Santa Barbara lies in UTM Zone 11, and that the boundary of Zone 10 is at the 120th meridian just West of Goleta, but only if you live in Santa Barbara! Other aspects of grid references may or may not easily commit themselves to memory, but if they do are useful for all sorts of basic fact retrieval and navigation. Effective systems promote such recall, and exploit it. Nevertheless, measurement of this property seems almost impossible without resorting to qualitative methods.
Secondly, many applications of coordinates focus on their use for the extraction of successive sample locations directly from random numbers applied to the coordinates and their ranges. To be suitable, a grid system should allow the extraction of samples in random, systematic, hierarchical or other appropriate sampling methods. Resampling coordinates is often an important part of multi-scale cartography, therefore support for multiple representations or multiple display scales is desirable. If this happens as coordinates are resampled, then generalization is possible by simply weeding duplicate coordinates.
Within a system, accuracy is defined by repeatability. A grid system should be able to return a user or navigator to the exact same location, independently of minor details such as rounding error, algorithm implementation, and pixel resolution. A measure might be to locate a set of points one thousand times each, and to quantify the average positional error involved in repetition. Even with computer algorithms differences emerge. With human interpretation and with look-up solutions, errors can be significant.
Finally, error is both a global and a local property of grids. Aggregate accuracy measures mask the extremes and spatial distribution of error. Efforts should be made to portray not just the amount of error, but also its spatial distribution. This is often possible with quite traditional cartographic methods (Clarke and Teague, 1998).
Table 3. Summary of the Metrics for Global Grid Comparison
| Dimension | Metric | Value | Units | Geographic Coordinate Example |
| Universality | Proportion of earth's surface covered by grid | Ratio (0.0-1.0) | None | 1.0 |
| Universality | Recoverability of grid system origin monument and standard dimensions | Boolean (2 values) | Yes/No | {0, 1} Units are ISO defined |
| Universality | Proportion of parameters and constants tied to International or national standard | Ratio (0.0-1.0) | None | 1.0 Assuming metadata (e.g. ITRF, WGS84) |
| Universality | Number of International or National Standards referenced by specification | Greater than or equal to zero | Standards | 2 (Ellipsoid, International Meridian Conference) |
| Authority | Number of bibliographic references to grid system | Greater than or equal to zero | References in Snyder bibliography | 351 |
| Authority | Number of references on World Wide Web | Greater than or equal to zero | Number of hits using altavista with "geographic coordinate"on 3/21/00 | 1,305,095 |
| Authority | Number of catalog entries | Greater than or equal to zero | Search of "magazine and journal articles" in all UC libraries on 3/21/00 for "geographic coordinates" under subject keywords | 27 |
| Authority | Entries in textbook index | Greater than or equal to zero | Number of pages referenced in index for Sixth Edition of Robinson et al. "Elements of Cartography", under "geographical coordinates", "latitude", and "longitude" | 11 |
| Authority | Degree of conformance to standard | Boolean | Assumed, since ISO references. | 1, Yes |
| Authority | Number of standards that reference the system | Greater than or equal to zero | Standards | Unknown |
| Succinctness | Number of Digits in Geocodes | -90.0 to 90.0 for latitude, -180.0 to 180.0 for longitude | Degrees, decimal or degrees, minutes and seconds with decimals | 22 (including decimals , a space, and 2 sig. figs. for DMS) |
| Succinctness | Number of ASCII characters per point with full geocode | Greater than or equal to zero | ASCII characters | 27 (includes EOL) |
| Succinctness | Coordinate Digit Density Function | Graph (one value per significant digit) | None | NA |
| Succinctness | S (entropy measure based on CDDF) | 0-1.8 | None | NA |
| Succinctness | Number of Algorithm Steps for retrieval | Greater than one | Steps | NA |
| Succinctness | Number of computations to ASCII conversion | Greater than one | Computations | NA |
| Succinctness | Number of look-ups performed | Greater than or equal to zero | Look-ups | NA |
| Succinctness | CPU time for conversion | Greater than zero | seconds | NA |
| Succinctness | User encoding and decoding time | Greater than zero | seconds | Needs human subject tests |
| Definitiveness | Overlap as a proportion of total space covered by grid | Greater than or equal to zero | Ratio | 0.0 for latitude
approx. 0.001 for longitude |
| Definitiveness | Weighted Overlap as a proportion of total space covered by grid | Greater than or equal to zero | Relative value, reflecting multiple counts | 0.0 for latitude
Infinity at 90N and 90S, 0.0 elsewhere |
| Definitiveness | Similarity coefficient for adjacent cells/points | Ratio of bitwise mismatch to mismatch + match (0.0-1.0) | Ratio | At 2 sig. fig for seconds, 0.9091 |
| Exhaustiveness | Range of resolutions covered | Two values, both representative fractions or ground distances | Ratios | 1:400,000,000 to 1:1 |
| Exhaustiveness | Range of precision | Significant Digits or parts per million | Digits/PPM | 5 (whole degrees) to 17 |
| Exhaustiveness | Proportion of earth covered at finest resolution and precision | Greater than zero | Ratio | 1.0 |
| Exhaustiveness | Compared to Geographic, pixel loss and duplication ratios | Loss 0.0-1.0
Duplication greater than zero |
Ratio | NA (comparison base) |
| Exhaustiveness | Ratio of atom to resolution | Greater than zero | Ratio (smallest desired resolution/precision) | 1m/0.31 m = 3.23 |
| Hierarchy | Number of reprojections within system | Greater than or equal to zero | Different projections/central meridians, points of tangency or secancy | 0 |
| Hierarchy | Number and length of joints | Greater than or equal to zero | Count | 0 |
| Hierarchy | Number of recursions from base to atom level | Greater than one | Recursion levels | 3 (for DMS) |
| Uniqueness | Average number of significant digits in coordinates that distinguish between adjacent cells or points | Greater than one | Digits | 1 |
| Uniqueness | Coordinate Digit Density Function for point pairs | Graph | NA | NA |
| Uniqueness | Match ratio for adjacent coordinates | 1-(mismatch/(match + mismatch)) 0.0-1.0 | None | At 2 sig. fig for seconds, 0.9091 |
| Intuitive Understanding | Number of facts that explain system | Greater than one | Facts | 8 |
| Intuitive Understanding | Number of parameters externally defined (magic numbers) | Greater than zero | parameters | 4 |
| Intuitive Understanding | Length of explanation/documentation | Greater than zero | Words (Source: Snyder Map Projections: A Working Manual) | C. 1000 |
| Intuitive Understanding | Time to achieve error free use | Greater than zero | days, minutes | NA |
| Intuitive Understanding | Educational level required | K-16 | Grade Level | 10 |
| Intuitive Understanding | Time to achieve explanation | Greater than one | minutes | 20 |
| Intuitive Understanding | Frequency of retraining | Greater than zero | months | NA |
| Intuitive Understanding | Memory recall of common geocodes | Binary, or Human subjects derived error rate | Yes/No or proportion of error | NA |
| Tractable | Availability of Method | Formulae or algorithm in literature/web | Yes/No | Yes |
| Tractable | Size of computer program for use | Smallest available computer program | Bytes | NA |
| Tractable | Steps in program logic | Lines of code | Lines | NA |
| Tractable | Program execution time | CPU or user time | seconds/point | NA |
| Tractable | Supports sampling and generalization | Boolean | Yes/No | Yes |
| Accurate | Test against independent source of higher authority | 1-(mismatch/(match + mismatch)) 0.0-1.0 | None | 1.0 (self) |
| Accurate | Forward to inverse transformation comparison | 1-(mismatch/(match + mismatch)) 0.0-1.0 | None | 1.0 (self) |
| Accurate | Repeatability | Proportion in error | None | 1.0 (assumed) |
| Accurate | RMS or other single accuracy value for whole data set, as projected | distance or standard deviation | meters | 0.31 m |
Analytical cartography can serve in comparing global grids to conduct meta-analysis of entire systems. The metrics and methods proposed can serve to illustrate possible enhancements, improvements and modifications to existing grid systems that may be of considerable benefit to map producers and users alike. Whatever the outcome, the current era of Internet and World Wide Web based cartography will ensure that the user, rather than the cartographer, surveyor, or geodesist will increasingly influence the future of the mapping sciences. Occam's razor has been proposed as applicable to global grid systems, that is, given two equally useful and powerful grid systems, the better one is the simpler of the two. User demand assessment and user testing are only now becoming regular tools in the cartographer's toolbox. Web mapping both demands immediate solutions to the inadequacies of particular grid systems and provides a somewhat objective means by which user testing can be conducted rapidly and in sufficient numbers to move beyond the currently favored "30 geography students" that human subjects tests of mapping applications tend to use.
The future, quite clearly, will reward those systems that meet their
Web searching demands with de facto acceptance and therefore authority.
For over a century, cartography has allowed the competitive coexistence
of global grid systems devised for different applications. As surveying
and mapping yield to mobile mapping applications such as navigation and
high-precision positioning, it is hoped that the methods and metrics proposed
here can lead to some effective choices for the future based on analysis
and quantitative methods rather than subjectivity and bias.
Clarke, K. C. (1995) Analytical and Computer Cartography.
Englewood Cliffs, NJ: Prentice Hall.
Clarke, K. C. and P. D. Teague (1998) "Cartographic Symbolization of
Uncertainty" Proceedings,
ACSM Annual Conference, March 2-4, Baltimore, MD. (CD-ROM)
Dretske, F. I. (1999) Knowledge and the Flow of Information. Stanford University: CSLI Publications.
Dutton, G. H. (1999) A hierarchical coordinate system for geoprocessing and cartography. Berlin ; New York: Springer.
Goodchild, M. F. (1994) "Criteria for evaluation of global grid models for environmental monitoring and analysis", Handout from NCGIA Initiative 15, see Spatial Analysis on the Sphere: A Review, by Rob Raskin, NCGIA Technical Report 94-7. Copy courtesy of Waldo Tobler.
Goodchild, M. F. and Gopal, S. eds. (1989) Accuracy of Spatial Databases. London: Taylor and Francis.
Howse, D. (1997) Greenwich Time and the Longitude, London: Philip Wilson.
Kimerling, A. J., K. Sah, D. White and L. Song (1999) "Comparing Geometrical Properties of Global Grids", Cartography and Geographic Information Systems, vol. 26, no. 4, pp. 271-88.
Monmonier, M. S. (1995) Drawing the line : tales of maps and cartocontroversy, New York :H. Holt.
Mulcahy, K. A. (1999) Spatial Data Sets and Map Projects: An Analysis of Distortion. Ph.D. Dissertation, City University of New York: University Microfilms: Ann Arbor, MI.
Mulcahy, K. A. and K. C. Clarke. "Cartographic Visu alizations of Map Projection Distortion: A Review", Car tography and Geographic Information Science, vol 28, no. 3, pp. 167-181.
Robinson, A. H. et al. (1995) Elements of Cartography. New York: J Wiley. 6th. ed.
Shannon, C. (1948) "The Mathematical Theory of Communication", Bell System Technical Journal, July/October.
Tobler, W. 1970. "A Computer Movie Simulating Urban Growth in the Detroit
Region." Economic Geography
46(2):234-240.
Tobler, W. R. and Z. Chen (1986) "A Quadtree for Global Information Storage", Geographical Analysis, vol. 18, no. 4, pp. 360-371.
Tobler, W. R. (2000) "The development of Analytical Cartography: A Personal Note," Cartography and Geographic Information Systems, Vol. 27, No. 3, pp. 189-194..
Tukey, J. W. (1977) Exploratory Data Analysis. Reading, MA: Addison-Wesley.